HANDBOOK OF THE INTERNATIONAL COMPARISON PROGRAMME

Annex II - METHODS OF AGGREGATION

1. The present annex begins with the Geary-Khamis method of aggregation, explaining some of its advantages and disadvantages. It then compares the G-K results with several other methods of aggregation to illustrate some of the differences.

2. The valuation of a country's output in international prices can be written as:

(1)


and where the p _is are the international prices for each of the basic headings and rgdp_j is GDP of country j valued at those prices. The particular contribution of Geary was to define the international prices in such a way that they would produce an overall PPP for a country that was consistent with the prices. The definition of the PPP in the ICP is:

(2)


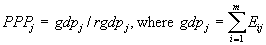
where E_ij is the expenditure in national currency on basic heading i by country j. That is, the purchasing-power parity over GDP is the ratio of the GDP of a country in national currency to its GDP in international prices.

3. For Geary there were actual quantities and prices associated with the agricultural output that he was concerned with valuing across countries. The international prices would be in a numeraire currency, such as the dollar, and the international prices would be so many dollars per unit quantity, say, ton of rice. In the ICP, there are basic heading parities, PPijS, that have been generated by EKS or CPD. These basic heading parities have the dimension of units of currency of country j to the numeraire currency for the basic heading.
4. This means that the interpretation of quantity and price at the basic heading level are not tons and rupees per ton. Rather, the quantity in the G-K technique as used in the ICP is what is termed a notional quantity. It is defined as:

(3)


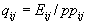
Each country's expenditure for a basic heading is converted to the currency of the numeraire country; it is termed a notional quantity because it serves the function of a quantity with its values at numeraire country prices.

5. One might ask why one cannot simply add up the notional quantities for each basic heading for a country to get a GDP in a common currency. The answer is that the result would use the relative prices between each basic heading that prevailed in the numeraire country. This means that the total would depend on which country was chosen as numeraire, and the result would not be base country invariant.
6. In the G-K system, the international price for heading i is defined as:

(4)


Equation (4) has been written as a weighted sum of the ratios of the heading parities to the aggregate PPP. The weights used to obtain the international prices typically are the notional quantities. Usually, the expenditures (E_ijS) entering into equation (3) are the total expenditures of a country, though alternative weights have been used. a/ For each country this is a ratio that will centre on 1.0 because in the Geary system the PPP_j is a weighted average of the basic heading parities, where the weights are the notional quantities.

7. An important feature of the G-K system is illustrated in equation (5), where the denominator of equation (4) is brought to the left-hand side:

(5)


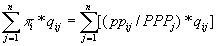
Each side of equation (5) is a measure of the contribution of output of a basic heading to regional or world GDP. It is only in the G-K system that the valuation of quantities at international prices is consistent with their basic heading parities and expenditures, as well as the overall purchasing-power parity of each country.

8. Equations (1) and (4) represent the complete G-K system when PPP_j and q_ij are defined as in equations (2) and (3). When m is over 150 and n is over 60, this appears to be a large system to solve. However, it turns out that the easiest way to solve the system is by iteration; and it also turns out that the iterative procedure is itself instructive, as the following discussion is intended to show.
9. The basic data are the expenditures (E_ijS) and parities (pp_ijS) at the basic heading levels, and from these the q_ijs can be derived. Consider an iteration that begins by initially setting each PPP_j equal to the exchange rate. For example, if the United States were the base country, then its initial PPP would be 1.0 and the initial PPPs for the other countries would be their exchange rate relative to the dollar. Then a set of international prices can be estimated using equation (4). These p _is can then be plugged into equation (1) and then equation (2) to estimate a set of PPP_jS. The process can then be repeated beginning with the new PPP_iS. The iteration will be complete when the difference between the initial set of PPP_jS and the end set is very small. Typically, in eight iterations the differences will only be observed at the fourth decimal place. It is unlikely that when the last iteration is complete the new PPP for the United States will equal 1.0. The system is then normalized so that each new PPP is adjusted so that the United States value will be 1.0, and the p _is appropriately scaled so that, for the United States, gdp and rgdp as obtained from equation (1) are equal.
10. While one can begin the iteration with any set of values, there is another way to begin that is also instructive. Consider setting each of the initial international prices (p _is) equal to 1.0. The same loop can then be followed, estimating the PPPjs when the p _is are all 1.0, and work back through the system to obtain a new set of international prices, and a new set of PPPs and so on. A normalization as described in paragraph 9 would also be carried out to make the PPP of the base country 1.0. Beginning with all international prices equal to 1.0 is equivalent to using the relative price structure of the numeraire country. The fact that the final set of international prices will differ substantially from 1.0, no matter which country is numeraire, again illustrates why one cannot simply sum up the notional quantities given in equation (3).
11. This discussion should also make clear that the international prices of the ICP centre around 1.0 and are used to value a quantity that has no natural dimension, such as a kilogram, but has a notional character depending on the numeraire currency. b/ The iteration procedure also illustrates how the Geary system achieves additivity across countries and basic headings to achieve matrix consistency.
12. As discussed in the text the major advantage of the Geary system is that the international prices are analogous to the prices used to generate the national accounts of an individual country. In the Geary formulation, large rich countries receive more weight in determining international prices used to value quantities in each country. This means that the structure of international prices will tend to be closer to those of rich countries. There is also usually an inverse relationship between price and quantity across countries, so that items that are expensive in poor countries, for example, will be consumed in relatively small quantities and vice versa. The G-K price structure will tend to value the large quantities of relatively inexpensive items in poor countries, such as services, at higher prices. Conversely, those items that are relatively cheap in rich countries, such as transport equipment, will be valued at international prices closer to their national value. This effect is present in all of the aggregation systems since it is part of the world economic structure that the ICP is attempting to represent.
13. However, the international price systems that are explicit or implicit in other systems are usually closer to middle-income countries because the weights used are not in proportion to country GDP. As a consequence, the G-K system tends to lower the income of rich countries relative to poor countries more than the other aggregation methods. Some regard this as a desired result stemming from the national accounts basis of the G-K system, while others regard it as a drawback. c/

14. One type of aggregation system, devised by D. Gerardi, that was used by EUROSTAT was based on international prices used to evaluate notional quantities, as in equation (1) above. The Gerardi system was compared with the G-K system by Hill (1982, pp. 51-59), and that discussion will not be repeated here. The objective of both the Gerardi system and other international price systems with which EUROSTAT has experimented has been to retain an additive system that does not use international prices close to those of larger countries. Another way of putting this is to say that there are those who want matrix-consistent comparisons, but do not want to use a set of prices that are quantity weighted as in national accounts. Gerardi's international prices, for example, were initially based on equal weights to the pyqs of each country.
15. Another motivating factor for those seeking alternatives to the G-K system that are inherently additive is that G-K is a simultaneous system that requires all information from all countries before it can be calculated. A price change in one basic heading can, in principle, change the estimates of other basic headings. d/ Also, results of the G-K system can change as the number of countries included in the aggregation changes, though this is also true for most other aggregation systems.

16. Erwin Diewert has made an extensive review of indexes that might be used in international comparisons, and has come up with a class of what he terms superlative indexes (Diewert, 1978). What he finds is that indexes built up from Fisher-type comparisons between two countries have a number of desirable properties that flow from the theory of consumer choice. From this it follows that a multilateral index based on Fisher binary indexes, such as the EKS system, appears to have more theoretical rationale than the G-K system.
17. While Diewert's arguments provide some support for EKS, the issue is not so easily resolved. First, 30 to 40 per cent of expenditures on GDP are typically not chosen on the basis of relative prices. That is, most government expenditures and much of investment is not allocated on the basis of the principles underlying consumer choice. It is not claimed that EKS, G-K or any other system is necessarily better for comparing these expenditures, but that the theory of consumer choice is applicable to a portion of GDP only.
18. The second point relates to additivity. There are several systems that have been used that, like EKS, produce an overall comparison for all the basic headings entering the aggregation. One of these systems, the van Yzeren system, was proposed for the European Coal and Steel Community and another, the Walsh or expenditure weight system, has been used in Latin American comparisons. e/ The EKS system, as well as the Walsh and van Yzeren systems, provide a PPP over GDP or whatever aggregate for which they have been computed. However, they do not have an implicit system of international prices, so there is no explicit allocation of the expenditures within the aggregate and no inherent additivity. It is simple enough to impose additivity by, say, distributing the expenditures on GDP obtained by EKS across the categories according to the distribution of those expenditures in national currencies. The disadvantage of this is that the method is arbitrary and no information about the price structure in other countries is used in comparing the structure of expenditures in one country with those in another.
19. One further point is that for some purposes the only number sought is for an aggregate such as consumption. One might, for example, want to use the PPP for consumption to compare real wages across countries. In this case, an EKS aggregation may be preferred to the G-K method for two reasons. First, since additivity is not needed in this example, one drawback to using EKS is removed. Secondly, the implicit weighting involved in EKS is equal among countries so that for converting wages across countries it may make more sense to think of using a PPP that assigns the same importance to the market basket of each country. (The latter weighting system can also be achieved by G-K.)
20. To give some impression of what differences are involved in the various methods, results are given below from the phase III report for six countries, spanning the range of per capita incomes in the world. The entries give the per capita income of each country relative to the United States as 100 for each country.

Country per capita GDP, 1975 (US = 100)

Method	India	Kenya	Colombia	Republic of Korea	Japan	France
1. Binary-Fisher	6.0	5.8	19.7	17.2	67.5	80.2
2. Geary-Khamis	6.6	6.5	22.6	19.9	68.6	81.9
3. EKS	5.7	5.4	19.9	17.8	65.3	81.1
4. Walsh	6.4	4.8	19.5	17.6	66.1	80.0
5. Van Yzeren	5.7	5.4	19.9	17.7	65.3	81.0
6. Gerardi	5.7	5.8	20.4	18.5	66.6	77.8
7. Exchange rate	2.0	3.4	7.9	8.1	62.3	89.6

Source: Kravis, Heston and Summers, 1982, pp. 96-97.

21. The differences between the first six rows for any one country are less than 5 per cent for Japan and France, and less than 15 per cent for the remaining countries. A seventh row is also provided for the exchange rate conversions, indicating that all of the other methods are much closer to one another than to use of the exchange rate, and for Japan and France, the deviations are over 10 per cent and in opposite directions. Thus, while results of the different methods can vary from one another, their general orders of magnitude for each country and variation across countries tell a fairly consistent story.
22. It would be nice if there were a simple conclusion to be drawn from this discussion, but that would imply that somehow the ICP had solved the index number problem, which it assuredly has not. One longs for one measure because that would be simple to explain to users, especially users providing resources for the work. It is also tidier to have only one result. However, because there are a variety of uses for which the ICP results are desired, for the present, more than one result will be produced, though in official publications the differences will be minimized.

23. Some expenditure categories can be negative, such as change in stocks or the net foreign balance. These categories do not make much sense in any method using international prices because the Geary system, for example, is based on positive quantities and prices. Therefore, in the G-K system, the actual solution is carried out over the non-negative basic headings. The parities assigned to the net foreign balance and the net expenditures of residents abroad is the exchange rate. (A different treatment is made for countries with a large amount of tourist expenditures, such as Austria, where net expenditures of residents abroad may be distributed among the important headings, and no expenditure is retained in that heading.) In phases I to III of the ICP, the international price for these two headings was defined as in equation (4), but has since been assumed to be 1.0.
24. For change in stocks, a parity is calculated from the G-K result based on those basic headings that are commodities. That parity is assigned to the change in stocks. The international price for the category is then calculated from equation (4) above. Any normalization to make the PPP of the base country 1.0 is then carried out involving the international prices of all basic headings. In the comparisons of methods given above, the actual comparison is over the non-negative categories, since this appeared to put all methods on the most comparable basis.

a/ For the world comparisons in phases I-IV, countries were assigned additional weight to reflect the importance of countries not included in the benchmark comparisons. The total expenditures of a country were termed its supercountry weight, and the sum of all supercountry expenditures would be world GDP. One reason for using supercountry weights was to estimate the international prices that were implicit in world GDP. Since the G-K result does depend on the number of countries in the calculation, the use of supercountry weights was designed to approximate the international prices if all countries in the world were participating in the ICP. This in turn should, in principle, make the results from earlier benchmark ICP comparisons, when relatively few countries participated, better approximate later comparisons involving more benchmark countries.
In the Geary system, it is also possible to use per capita expenditure weights or other weighting systems, For example, one could assign equal weights to each country over all expenditures and in effect use the percentage expenditure for each basic heading as the country weight. The discussion in this annex assumes that the overall weight for each country is their GDP, or supercountry GDP.

b/ The international prices will depend on the numeraire country chosen. This point is discussed in Kravis, Heston and Summers (1982, pp. 94-95). Two other technical points may be noted. First, some regions have chosen to use a numeraire currency outside the region, as, for example, Africa. In the African comparisons, all prices and expenditures are initially converted into United States dollars at exchange rates. In the African study, no single country is used as the base, but rather the average of all countries is used. While the results of the African study are presented in dollars, this does not make them comparable with other countries, such as the United States, because dollar conversions have only been carried out at exchange rates.
A second point is that when an average of a group of countries is used, as in Africa or the European Communities, there will still be a set of international prices implicit in the calculation. In the African case, the system would be normalized to make the sum of expenditures of all headings and all countries converted at exchange rates equal to the sum of all notional quantities valued at international prices. For any particular basic heading, this equality would not hold, and the ratio of the sum across all countries of the basic heading notional quantities valued at international prices to their value at exchange rates would be the international price for that basic heading.

c/ Usually, the G-K results are criticized because they depart from Fisher binary results, being closer to the Laspeyres than the Paasche estimate for poor countries. However, the binary comparisons being used as a reference weight each country the same. The EKS system, which is an indirect least squares type of estimate from the binaries, naturally comes closer to the Fisher result than does G-K. However, Prasada Rao has shown that, if a binary is done using the GDP weights of the G-K system, then the multilateral G-K is a direct least squares estimate based on the binaries and, of course, comes much closer to the G-K binaries than does EKS. The point, then, is that it is really the weighting system that produces more difference between methods than other factors (see Prasada Rao (1972)).

d/ This can readily be seen by examining equation (5). A price change affects a PPij and that may affect the PPPjS and work itself through the entire system. Any other system that was matrix consistent would also be affected. Systems like EKS would be affected in the aggregate but because there is no explicit estimates of basic heading quantities in EKS, there is no visible effect at the detailed level.

e/ These systems are discussed in Kravis, Kenessey, Heston and Summers (1975), pp. 66-68.